UK Mortgage Repayment Calculator With Amortisation
Use this calculator to figure out what your monthly loan repayments will be for either fixed-rate or interest only loans. You have the ability to schedule future interest rate changes in your calculation, which will help you see how your loan payments will change if rates rise. If rates fall you can of course remortgage again at the lower rate when your fixed introductory period has concluded.
Usage Instructions
- Basic Loan Structure: Enter the price of the home, your down payment and how loan your loan amortisation schedule lasts.
- Fixed-Rate Details: Enter your introductory fixed rate, rate change frequency, anticipated rate changes, and interest rate cap.
- Interest-Only Details: Enter your introductory rate, rate change frequency, anticipated rate changes, and interest rate cap.
- Printable Report: Click on the "printable schedule" button at the bottom of the calculator to create a printable amortisation schedule for your loan scenarios.
Calculate Your Loan Repayments
How Amortisation Works: Tracking Mortgage Payments
Mortgages are a major financial commitment that people pay for a long time. In the UK, the typical mortgage term lasts for 25 years. Thus, it’s important to arrange your finances and track your monthly payments accordingly. To do this, you must acquaint yourself with the concept of amortisation, and how this accounting method determines your mortgage payments.
Furthermore, you might want to consider making overpayments on your home loan. Just be wary of early repayment charges to avoid extra costs. Doing so allows you to pay off your mortgage earlier, which reduces your total interest expenses. We’ll also touch on the importance of remortgaging your loan. This ensures you receive favourable rates even after your initial fixed-rate mortgage is through. Overall, understanding amortisation will give you a better grasp of planning your mortgage expenses.
Mortgage Amortisation Formula
Here is the formula for calculating regular amortising monthly repayments.
Mortgage Payment = P x (r / n) x [(1 + r / n)^n(t)] / [(1 + r / n)^n(t) - 1]
where
- P = principal
- r = mortgage interest rate as a decimal
- n = number of payments per year (12 for monthly)
- t = loan term in years
Here is the calculation for a 3% APR loan over 25 years
£180,000 x (.03 / 12) x [(1 + .03 / 12)^12(25)] / [(1 + .03/12)^12(25) - 1]
£180,000 x 0.0025 x [1.0025^300] / [(1.0025)^300-1]
£180,000 x 0.0025 x 2.11501955766 / (2.11501955766 - 1)
£450 x 2.11501955766 / (1.11501955766 ) = £853.58/mo
A person could do this calculation by hand, or use the calculator on our homepage to do it faster automatically.
Each time a mortgage's rate changes the above calculation begins anew. So, for example, if after a 5-year introductory rate of 3% the loan jumps to 3.6% you would calculate the new payments likeso:
£153,909.86 (balance from the orignal mortgage after 5 years of payments) at 3.6% APR (the new rate) loan over 20 years (25 years less the 5 years already paid)
£153,909.86 x [(.036 / 12) x [(1 + .036 / 12)^12(20)] / [(1 + .036/12)^12(20) - 1]
£153,909.86 x (0.003) x [1.003^240] / (1.003^240 - 1)
£461.73 * 2.05222004333 / (2.05222004333 - 1)
£461.73 * 2.05222004333 / 1.05222004333 = £900.54
The above formula is for an amortising loan. And each time rates reset you would do the calculation above. The subsequent year if rates changed again you'd insert the balance from the end of that year, shift the loan term from 20 years to 19, and insert the new interest rate.
Each calculation is easy, but doing it by hands dozens of times can get tiring.
The maths on interest-only payments is even easier.
Interest Only Mortgage Payment = P x (r / n)
£180,000 * .03 / 12
£180,000 * 0.0025 = £450/mo
As rates changed on an interest-only loan you could calculate new payments the same way using the above simple formula. If you ever made any extra payments then you would run the calculation again with the new balance, but otherwise the balance on interest-only loans doesn't change as one is just paying the interest as it accrues.
Explaining Amortisation

Amortisation is the process of distributing payments evenly within an agreed term to pay off a debt. It’s an accounting technique used in loans that come with a specific loan amount (capital), interest rate, and term duration. The periodic payment is calculated based on these three factors, which is usually paid in monthly instalments. Thus, amortisation is a characteristic often found in fixed-rate loans.
When your debt amortises, it ensures your loan’s capital and interest balance is reduced to zero by the end of the term. Note that both the words amortisation and mortgage share the Latin noun mors, which means death. In this respect, when a mortgage amortises, it literally means making instalment payments to kill off or eliminate debt.
When the interest rate is fixed for a set period, the resulting monthly payment stays the same. This is characterized as a regular amortising loan. For instance, if you obtain a 5-year fixed-rate mortgage, you’re guaranteed the same monthly payment for the entire 5-year term. The predictable payments make managing costs more convenient for borrowers. For this reason, compared to standard variable rate mortgages (SVR), fixed-rate mortgages have become more popular in the UK. Fixed-rate mortgages also typically have lower interest rates than SVR mortgages.
When you obtain a mortgage, lenders use an amortisation schedule to monitor your payments. This is a table that breaks down the precise amount you must pay, and how many payments you must make within the term. Repayment mortgages require you to pay both the capital and interest balance, which is the full monthly payment in the amortisation schedule. On the other hand, if you take an interest-only mortgage, the amortisation schedule will only calculate the required interest payments per month.
For instance, if you take a 5-year fixed-rate mortgage, your amortisation schedule comes with 60 monthly payments of the same amount. The table also details the exact amount that goes toward your capital balance (the amount you borrowed) and interest per pay period. Meanwhile, if you take a 3-year interest-only mortgage, your amortisation schedule will only require 36 monthly interest payments for the designated term.
After the fixed-rate or interest-only mortgage ends, you have the option to remortgage to a fixed-rate term, or any type of mortgage you see fit. Otherwise, your rate will shift to the standard variable rate mortgage (SVR), which usually has a higher rate. Consider remortgaging to a fixed-rate loan to avoid the higher rate, which results in expensive monthly payments.
To generate a sample amortisation table, use the above calculator.
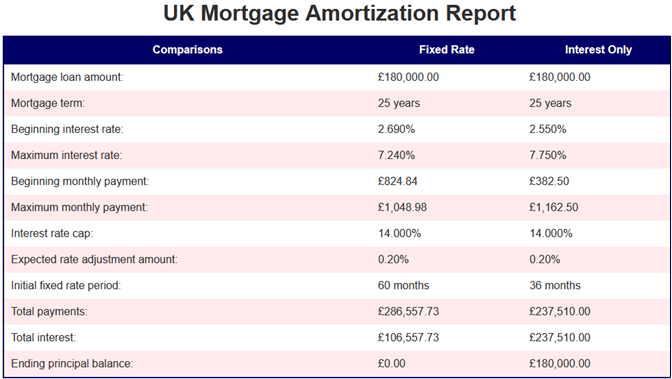
The following image is a sample amortization schedule for the first year of a mortgage. It includes payments for a fixed-rate term side by side an interest-only term. The calculator also generates a comparison report between a fixed-rate mortgage and interest-only mortgage.
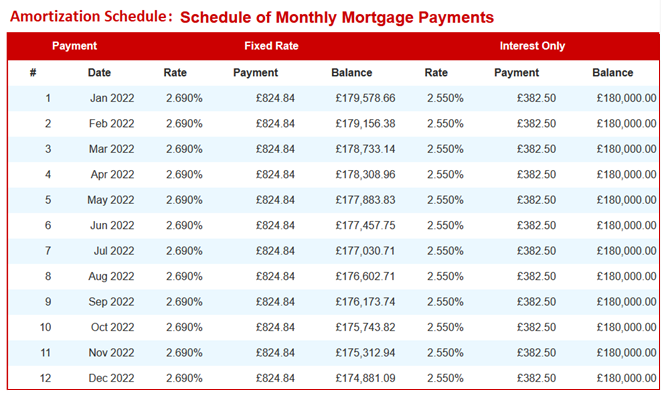
Negative amortisation occurs when a borrower makes a minimum payment that does not account for all interest charges due under the current interest rate. This unpaid interest is deferred and added to the capital loan balance. As a result, negative amortisation occurs. For instance, if you’re paying an interest-only mortgage, make sure you are making adequate monthly interest payments.
With negative amortisation, if your capital balance keeps increasing, it might exceed the original amount you borrowed. You’ll end up owing more on your mortgage than the home’s price. This will make it harder to pay your mortgage. Even if you sell the house, the proceeds from the sale will not be enough to pay off your mortgage. Be sure to make the right monthly payments that cover your loan’s interest costs.
How Fixed-rate Mortgages Work in the UK

Historically, standard variable rate mortgages (SVR) were the default mortgage product in the UK. With an SVR, the rate rises and falls based on the Bank of England (BoE) base rate. It’s also subject to change upon the lending institution’s discretion. When interest rates decrease, borrowers could take advantage of affordable monthly payments. But in recent years, as SVR interest rates rose, many consumers found fixed-rate mortgages more appealing. Since 2016, fixed-rate mortgages have become the most preferred mortgage in the UK, especially for first-time homebuyers.
According to the Bank of England, over half of mortgages that originated in Q4 of 2019 had 5-year fixed interest rates or longer. On December 1, 2020, the average rate for a 5-year fixed mortgage was 2.69%, while an SVR had an average rate of 4.41%. That’s a huge difference of 1.72%. For this reason, most homebuyers are inclined to take fixed-rate mortgages.
UK mortgages generally amortize for 25 years. When you take a fixed-rate mortgage, your rate remains the same for the first 2, 3, or 5 years of the loan. Others may even take as long as 10 years. Currently, the most popular fixed-rate term is the 5-year option.
Short 2 or 3-year terms usually come with the lowest rates. But they do not provide stable payments for a longer period. If you keep taking short, fixed-rate deals, you must remortgage more often. This is a costly and time-consuming process. If mortgage rates increase after 3 years, you might end up with a higher rate even if you secure a fixed-rate loan.
Meanwhile, 5 to 10-year fixed terms have slightly higher rates than short, fixed terms. But as an advantage, you gain extended payment stability, which is a good trade-off for many homebuyers. You do not have to remortgage every couple of years. If rates increase, you’re guaranteed to make the same payments during the mortgage term. On the other hand, if interest rates eventually decrease, you cannot take advantage of cheaper mortgage payments. You must make the same monthly payment within the 5 or 10-year term.
To compare mortgage rates between SVR mortgages and different fixed-rate terms, refer to the table below. The following table shows average rates for UK mortgages as of December 1, 2020.
| UK Mortgage Type | Average Rate |
|---|---|
| SVR | 4.41% |
| 2-year Fixed | 2.49% |
| 5-year Fixed | 2.69% |
| 10-year Fixed | 2.85% |
The table shows that the highest mortgage rate is the SVR at 4.41%. Notice how fixed rates increase as the term is extended. The 2-year fixed term has the lowest rate at 2.49%, while the highest rate is the 10-year fixed term at 2.85%.
UK Fixed-rate Mortgages vs. US Fixed-rate Mortgages
Similar to the UK, most homebuyers in the US also prefer fixed-rate mortgages. The predictable payments make them more attractive options for borrowers. However, unlike UK mortgages, fixed-rate mortgages in the US market remain fixed for the entire life of the loan. This typically lasts for 30 years. While a fixed-mortgage in the UK can only last for 2 to 10 years, a fixed mortgage in the US is locked for the full 30-year term. If US borrowers want to change their rate and term, they must remortgage their loan, which is called refinancing in the US housing market.
Meanwhile, in the UK, you are obliged to remortgage your home loan every couple of years, depending on your chosen term. If you do not, your mortgage reverts into a standard variable rate mortgage (SVR) after a fixed-rate mortgage. This will result in unpredictable payments that change according to the Bank of England base rate, and the lender’s rate standards.
Before your fixed mortgage shifts to an SVR, you can remortgage into a new fixed rate term, or choose other mortgage options that helps maximise your savings. Remortgaging allows homeowners to secure a low rate with a new mortgage term to avoid the higher SVR rate. This remortgaging process can be repeated by the borrower until their remaining balance is paid off within the 25-year term.
The Main Components of Mortgage Payments

Mortgages come with three main variables that constitute monthly payments. These key components include the following:
- Capital – the loan amount, which is how much you borrowed
- Interest rate – based on the annual percentage rate (APR)
- Loan term – the agreed payment duration in years and number of payments
Capital
Prospective homebuyers must pass a mortgage affordability assessment when they apply for a home loan. Under this process, a lender evaluates your annual income, including your monthly personal and living expenses. It checks your outgoing payments and debt-to-income ratio by analysing your credit records. This incurs a hard review on your credit file.
Furthermore, the affordability assessment comes with a financial stress test, which simulates how income changes or fluctuations in interest rates impact your ability to make mortgage payments. Generally, the higher your income and the smaller your debts, the better your chances of securing a larger capital.
To gauge how much capital you might receive, consider taking a mortgage agreement in principle (AIP). This is a document from a lender stating the precise amount they are willing to offer. Unlike an official mortgage application, it does not require hard credit reviews. While this amount is non-obligatory for a lender, knowing the capital amount allows you to start searching for homes within a price range.
Note that qualifying for a bigger capital means taking larger debt. This logically results in higher monthly payments, which makes your budget harder to manage. For instance, suppose you qualified for a maximum capital amount of £350,000. If you purchase a home worth $350,000 and make a 10% deposit, your capital will be reduced to £315,000. In contrast, if you find a home priced a £300,000, and make a 10% deposit, this will significantly reduce your capital to £270,000.
Now, if you took a 5-year fixed-rate mortgage at 2.69% APR, how much would your initial monthly payment be? Refer to the table below.
5-year Fixed-rate Mortgage
Interest rate (APR): 2.69%
Mortgage loan term: 25 years
| Mortgage Details | Example A | Example B |
|---|---|---|
| Home Price | £350,000 | £300,000 |
| Capital Amount | £315,000 | £270,000 |
| Beginning monthly capital & interest payment | £1,443.47 | £1,237.26 |
| Total interest | £186,476.14 | £159,836.70 |
In this example, choosing a cheaper home (Example B) will reduce your capital by £45,000. Your monthly payment will be more affordable by £206.21. This will also save you £26,639.44 in total interest charges.
Assess your finances and determine a feasible capital before purchasing a home. Once you set this figure, do your best to follow it. Look for homes well within the price range and refrain from going over budget. The idea is to find property you can afford within your means. If you can make a higher deposit, consider paying at least 15% of the home’s price. This will substantially reduce your capital and even lower your initial interest rate.
Interest Rate
The fee banks charge to service loans is called the interest. For mortgages, this is based on the annual percentage rate (APR), which accounts for a percentage of your capital. Shorter fixed-rate mortgages come with lower rates, while longer fixed mortgages have higher rates.
The size of your capital impacts your mortgage’s interest charges. A higher capital results in higher total interest expenses. Likewise, reducing your capital by making a higher deposit will result in lower interest costs. A longer term also generates higher interest charges compared to a shorter term. Basically, the longer you take to pay a loan, the more interest your loan accrues.
Furthermore, borrowers also have the option to make interest-only payments. This means you can defer capital payments for a set period, then make a large lump-sum capital payment by the end of the term. This option is typically chosen by homebuyers who won’t stay long-term in a house and will eventually move to another location. When they sell the house, they can use proceeds from the sale to cover the capital balance.
How are interest rates determined? While your APR will depend on the type of mortgage you choose, lenders mainly assign mortgage rates based on the strength of your credit file. Generally, homebuyers with higher credit scores receive more favourable rates. Meanwhile, those with low credit scores are likely to receive higher rates and less favourable deals. Thus, it’s imperative to improve your credit score to obtain a lower mortgage rate.
Since credit scores vary per credit reference agency (CRA), it’s best to familiarise yourself with different ratings. This will tell you what’s a good credit score based on a specific CRA. The following chart shows credit score ratings for three of the most used CRAs in the UK: Experian, Equifax, and TransUnion.
| Credit Rating | Experian | Equifax | TransUnion |
|---|---|---|---|
| Excellent | 961 – 999 | 466 – 700 | 566 – 603 |
| Good | 881 – 960 | 420 – 465 | 604 – 627 |
| Fair | 721 – 880 | 466 – 700 | 566 – 603 |
Struggling with a low credit score? You can improve it by paying your bills on time, settling large credit card balances, and keeping your credit card balance low. Though improvements can take a couple of months to a year, never missing payments will significantly improve your credit score. Paying off large debts will also impact your credit record positively.
Before applying for a mortgage or any type of credit, make sure to review your credit report. This gives you a better idea of your current credit rating. CRAs are required to provide consumers with a free copy. You may contact your CRA’s official website to request a credit report. For more details on how to obtain your credit file, you may visit the Information Commissioner’s Office site.
Loan Term
The loan term specifies how long you must pay your mortgage. In the UK, the standard term for mortgages is 25 years. When you take a fixed-rate mortgage, your rate will remain locked for your chosen duration, which is typically between 2 to 10 years of the entire 25-year term. And the longer you secure a fixed-rate mortgage, the more stable your payments will be. This makes it easier to plan and manage your monthly budget. Long-term fixed-rate mortgages are ideal especially if SVR rates continue to be higher than fixed rates.
As a trade-off, expect to receive slightly higher rates on a 10-year fixed mortgage compared to a 2 or 3-year fixed mortgage. However, 10-year fixed mortgages still have a significantly lower rate compared to an SVR. This is usually a difference of nearly 2%.
Before the fixed-rate term is through, you may remortgage your loan to maintain a low rate and ensure fixed monthly payments. You have the option to keep remortgaging right before a fixed-term ends to avoid the variable rate mortgage.
With a low enough rate, some homebuyers elect to make overpayments to pay off their mortgage early. Making additional payments on your mortgage will reduce your capital faster. In effect, this will shorten your 25-year loan term. With early mortgage repayment, you can save tens and thousands of pounds on overall interest costs. However, just be wary of early repayment charges.
How much can I overpay? If you’re still in the introductory-fixed or discount period, most lenders allow you to pay 10% of your mortgage balance. But it’s best to check with your lender to know the exact amount allowed. Meanwhile, if you have a tracker mortgage, or your introductory deal has ended and you’re on SVR, you’re allowed to overpay as much as you can. Overpayments typically have penalty charges only during the introductory phase.
Mortgages, whether fixed or SVR, usually come with an early repayment charge (ERC). This is the required penalty amount if you repay your mortgage during the tie-in period, which is usually the introductory phase of the mortgage. It also applies when you overpay more than the allowed amount. The lender uses the fee to recoup some of the interest lost when you break the agreed term. Thus, be sure to overpay the allowed amount. ERC is a steep cost that can forfeit any savings from early repayment.
How Much Do Early Repayment Charges Cost?
Early repayment charges (ERC) take a percentage of your outstanding mortgage balance, which ranges between 1% to 5%. But to be sure how your ERCs are applied, verify with your lender. The penalty costs are usually tiered, which reduces with each passing year of the loan. For example, a 5-year fixed-rate mortgage might have a 5% early repayment charge on the first year. By the second year, it’s reduced to 4%, and down to 3% by the third year. On the fifth year, the early repayment charge will be 1%.
Suppose you took a 5-year fixed mortgage on a £100,000 loan. If you pay below the £10,000 limit, you won’t incur penalty fees. However, let’s say you paid £15,000 on the third year of the mortgage, which incurs a 3% penalty fee. You will be charged a 3% penalty on the £5,000 overpayment, which is £150. However, always verify your lender’s rule on overpayment charges to know you’re on the same page.
Under the Financial Conduct Authority (FCA), mortgage deals must state early repayment charges in cash value. Review your mortgage agreement or get in touch with your lender to verify the precise amount.
How Amortisation Works

Once you know the key variables that determine mortgage payments, you can start calculating your amortisation. You can use the following mortgage amortisation formula:
Mortgage Payment (MP) = C x (r / n) x [(1 + r / n)^n(t)] / [(1 + r / n)^n(t) – 1]
Where:
C = Capital or loan amount
r = Mortgage interest rate as decimal
n = Number of payments per year (12 for monthly payments)
t = Loan term in years
For instance, your home’s price is £250,000 and you made a 10% deposit worth £25,000. This reduces your capital to £225,000. Here’s the amortisation calculation at 3% APR for a 25-year term:
C = £225,000
r = .03
n = 12
t = 25
MP = £225,000 x (.03 / 12) x [1 + .03/12)^12(25)] / [(1 + .03/12)^(25) – 1]
= £225,000 x 0.0025 x [1.0025^300} / [(1.0025)^300 – 1]
= £225,000 x 0.0025 x 2.11501955766 / (2.11501955766 – 1)
= £562 x 2.11501955766 / (1.11501955766)
= £1,189.69 / 1.11501955766
= £1,066.98
In this example, the monthly payment is £1,066.97 for a £225,000 mortgage at 3% APR over a 25-year term.
However, this estimate only presumes the interest rate is the same for 25 years. Thus, each time your mortgage rate changes, you must start a new amortisation calculation. For instance, after the 5-year fixed-rate mortgage at 3% APR, the rate increases to 3.6% APR. Your capital balance is now £192,387.68. Because 5 years has passed, you have 20 years remaining in your loan term.
Here’s how you should apply the calculation:
C = £192,387.68
r = .036
n = 12
t = 20
MP = £192,387.68 x [(.036 / 12) x [(1 + .036 / 12)^12(20)] / [(1 + .036/12)^12(20) – 1]
= £192,387.68 x 0.003 x [1.003^240] / (1.003^240 – 1)
= £192,387.68 x 0.003 x 2.05222004333 / (2.05222004333 – 1)
= £577.16 x 2.05222004333 / (1.05222004333)
= £1,184.45 / 1.05222004333
= £1,125.66
With a new rate, your monthly payment will now be £1,125.66. Because the new rate is higher, despite the reduced capital balance, your monthly payment has increased.
Again, every time the rate changes, you must start a new calculation to know your monthly payment. All you have to do is verify the outstanding capital balance, new rate, and remaining term for the calculation. While this can be calculated manually, it’s faster to estimate your new monthly payment by using the above calculator.
How about interest-only mortgages? You can use the following formula to calculate interest-only payments. This calculation is easier since it only accounts for interest payments. Note that capital balance for the interest-only mortgages does not change. You are only calculating the payment as the interest accrues. The capital balance is paid in a lump sum by the end of the term.
Interest-only mortgage payment (IOMP) = C x (r / n)
Where:
C = Capital
r = Mortgage interest rate as decimal
n = Number of payments per year (12 for monthly payments)
For instance, suppose your capital balance is £225,000 and you took and interest-only mortgage at 3% APR. Here’s how the calculation will look:
C = £225,000
r = .03
n = 12
IOMP = £225,000 x (.03 / 12)
= £225,000 x 0.0025
= £562.50
In this example, your monthly interest-only payment will be £562.50. Likewise, once the interest rate on your mortgage resets, you start a new calculation to know the new monthly payment.
Calculating the Capital Paid
When you take a fixed-rate mortgage, amortization schedules break down how much of each payment goes toward the interest and capital. To calculate how much capital is paid, take your monthly payment and subtract the interest payment. The resulting amount is paid toward the capital.
For instance, suppose your monthly payment is £1,066.98 and you subtract the interest payment which is £562.50. The remaining amount will be £504.47, which is your capital payment.
Capital Payment = Monthly Payment – Interest Payment
= £1,066.98 – £562.50
= £504.48
Calculating the Current Capital Balance
To know how much you still owe, it’s important to keep track of your current capital balance. Just take your last capital balance then subtract your most recent capital payment. The resulting amount shows how much you still owe on your mortgage.
For example, if your last capital balance is £225,000 and your last principal payment is £504.48, your capital balance will be reduced to £224,495.53. This is your current capital balance until the next payment is made.
Current Capital Balance = Last Capital Balance – Latest Capital Payment
= £225,000 – £504.48
= £224,495.52
If we keep applying the amortisation calculation, we can create an amortisation schedule. The following table shows the amortisation schedule for the first 12 months based on our example. You’ll see how it’s easy to create an amortisation schedule with a fixed-rate mortgage.
Starting Capital: £225,000
Fixed interest rate: 3% APR
Loan term: 25 years
Monthly capital & interest payment: £1,066.98
| Payment no. / month | Monthly Payment | Capital Paid | Interest Paid | Ending Balance |
|---|---|---|---|---|
| 1 – Jan | £1,066.98 | £504.48 | £562.50 | £224,495.52 |
| 2 – Feb | £1,066.98 | £505.74 | £561.24 | £223,989.78 |
| 3 – Mar | £1,066.98 | £507.01 | £559.97 | £223,482.77 |
| 4 – Apr | £1,066.98 | £508.27 | £558.71 | £222,974.50 |
| 5 – May | £1,066.98 | £509.54 | £557.44 | £222,464.96 |
| 6 – Jun | £1,066.98 | £510.82 | £556.16 | £221,954.14 |
| 7 – Jul | £1,066.98 | £512.09 | £554.89 | £221,442.05 |
| 8 – Aug | £1,066.98 | £513.37 | £553.61 | £220,928.68 |
| 9 – Sep | £1,066.98 | £514.66 | £552.32 | £220,414.02 |
| 10 – Oct | £1,066.98 | £515.94 | £551.04 | £219,898.08 |
| 11 – Nov | £1,066.98 | £517.23 | £549.75 | £219,380.85 |
| 12 – Dec | £1,066.98 | £518.53 | £548.45 | £218,862.32 |
| Total | £12,803.76 | £6,137.68 | £6,666.08 | £218,862.32 |
Based on the first year of amortisation schedule, the total monthly payments would amount to £12,803.76, with £6,666.08 going to interest charges. After 12 months, the capital balance is reduced to £218,862.32.
When you review the table, notice how interest payments are higher than capital payments. Capital paid on the first payment is £504.48, while Interest paid is £562.50. But with each pay period, the capital payment increases incrementally, while the interest payment is reduced as well. By the twelfth payment, the capital paid increased to £518.53, while the interest paid decreased to £548.45. Over time, the capital payments will be larger than the interest payments, until the mortgage balance is completely paid off.
How Overpayment Affects Amortisation
While amortisation whittles away your mortgage balance, it does so in a very slow pace. Thus, other homebuyers prefer to make qualified overpayments to reduce their balance faster. This shortens their term and lessens interest charges. Making qualified overpayments can help you save thousands of pounds worth of interest on your mortgage.
Generally, lenders allow you to make an overpayment of 10% on your mortgage balance per year during the introductory period. Beyond that, you must pay early repayment charges. Consider talking to your lender about the allowed overpayments if you want to pay your mortgage sooner.
A Final Word

Keeping tabs on your monthly mortgage payments is crucial, especially if you decide to remortgage your loan every couple of years. You can do this by tracking your mortgage’s amortisation schedule, or doing your own calculations using the amortisation formula. Use the above calculator to conveniently estimate your monthly payments.
Amortisation is the process of making regular payments within a definite time to eliminate debt. It’s an accounting technique used on loans with a specific capital amount, interest rate, and loan term. While it’s easy to apply on fixed-rate mortgages, you must recalculate monthly payments on your amortisation each time your interest rate changes. Though lenders also keep a record of your amortisation schedule, you can create your own to monitor your monthly payments.
There are three key variables that determine your mortgage payments. This includes the capital, which is the amount you borrowed; the interest rate, which is based on an annual percentage rate (APR); and the loan term, which is the agreed repayment duration. Taking a mortgage with a large capital results in expensive monthly payments. If you can, make a higher deposit to reduce your capital and your interest rate.
As for the interest rate, borrowers are likely to receive a lower rate and a favourable deal if they have a high credit score. Generally, lenders prefer borrowers who pay on time, maintain low credit card balances, and have a stable source of income. Securing a low rate allows you to save on interest expenses. This also gives you room to make overpayments, which allows early mortgage repayment. But as a rule, watch out for prepayment penalties which may offset your savings.
As for the loan term, most UK mortgages have a payment duration of 25 years. Borrowers have the option to take fixed-rate mortgages, which last for the first 2 to 10 years of the mortgage. This is a popular option among homebuyers because it has significantly lower rates than the default SVR. It also provides stable, predictable payments which are a lot easier to budget. Before the introductory period ends, borrowers can remortgage to another fixed rate loan to avoid the higher rate on the SVR.
Check Out All of Our Free Online Calculators
Widgets | Affordability | Amortisation | Overpayment | Remortgage | About
Do you have feedback or questions? Email us
© 2019 — 2024 MortgageCalculator.UK — All Rights Reserved
